自伽利略于16世纪末第一次进行重力测量以来，国际众多科研机构（如美国宇航局(NASA)、德国航天局(DLR)、欧洲空间局(ESA)等）通过地面、海洋、空间等多种观测技术的联合已获得了全球的、规则的、密集的和高精度的地球重力场信息，因此全球重力场反演方法的优劣是决定人类对“数字地球”认识水平的关键所在。由于目前全球重力场反演方法自身的固有局限性，因此无论是各种方法单独还是联合均无法满足将来国际卫星重力测量计划中精确和快速反演全频段全球重力场的需求。因此，寻求新的、有效的和快速的全球重力场反演方法是本世纪国际地球物理学和大地测量学界的热点和亟待解决的难题之一。

自1957年10月4日第一颗人造卫星Sputnik-1成功发射以来，国际众多学者在利用卫星技术精密探测地球重力场方面取得了辉煌的成就。21世纪是人类利用卫星跟踪卫星（SST）和卫星重力梯度（SGG）技术提升对地球重力场认知能力的新纪元。重力卫星CHAMP（Challenging Minisatellite Payload，　 

2000.7.15发射）、GRACE（Gravity Recovery and Climate Experiment，2002.3.17发射）和GOCE（Gravity Field and Steady-State Ocean Circulation Explorer，2009.3.17发射）的成功升空以及GRACE Follow-On的即将发射昭示着人类将迎来一个前所未有的卫星重力探测时代（如图1所示）。

图1 国际地球重力卫星联测 ^[1]

卫星重力测量技术的实现是继美国GPS（Global Positioning System）星座成功构建之后在大地测量和地球物理领域的又一项创新和突破，它之所以被公认为是当前地球重力场探测研究中最高效、最经济和最有发展潜力的方法之一，是因为它既不同于传统的车载、船载和机载测量，也不同于卫星测高和轨道摄动分析，而是通过SST和SGG技术高精度感测地球重力场。地球重力场及其时变反映地球表层及内部物质的空间分布、运动和变化，同时决定着大地水准面的起伏和变化。[2] 因此，确定地球重力场的精细结构及其时变不仅是地球物理学、大地测量学、空间科学、天文学、国防建设等的需求，同时也将为全人类寻求资源、保护环境和预测灾害提供重要的信息资源[3]。

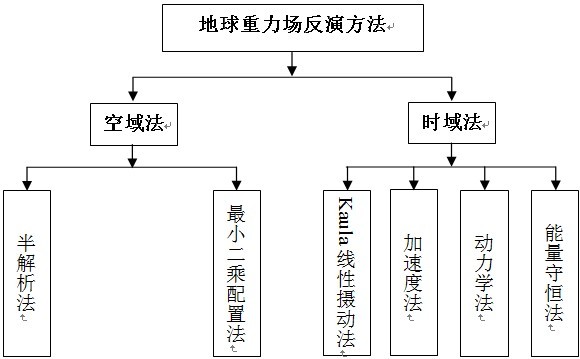
图 2 地球重力场反演方法分类

地球重力场反演是指通过分析卫星观测数据（GPS接收机的轨道位置及速度、K波段/激光干涉系统的星间距离及星间速度、星载加速度计的非保守力、恒星敏感器的卫星及载荷三维姿态、卫星重力梯度仪的重力梯度张量等）和地球重力场模型中引力位系数的关系，建立并求解卫星运动观测方程，进而反演地球引力位系数，最终目的是反演高精度和高空间解析度的地球重力场。如图2所示，在利用卫星重力测量数据反演地球重力场的众多方法中，按引力位系数反演方法的差异可分为空域法和时域法。第一，空域法是指不直接处理空间位置相对不规则的卫星轨道采样点的观测值，而将观测值归算到以卫星平均轨道高度为半径的球面上利用快速傅立叶变换（FFT）进行网格化处理，将问题转化为某类型边值问题的解，半解析法、最小二乘配置法等属于空域法的范畴。[4,5] 空域法的优点是因网格点数固定从而方程维数一定，可以利用FFT方法进行快速批量处理，因此极大地降低了计算量；缺点是在进行网格化处理中作了不同程度的近似处理。第二，时域法是指将卫星观测数据按时间序列处理，卫星星历直接表示成引力位系数的函数，由最小二乘、预处理共轭梯度等方法直接反求引力位系数。时域法的优点是直接对卫星观测数据进行处理，不存在任何近似，求解精度较高且能有效处理色噪声；缺点是随着卫星观测数据的增多，观测方程数量剧增，极大地增加了计算量。过去由于地球重力场反演方法的历史局限性和当时计算机技术发展的限制，为了减少计算量，因此空域法较为盛行。然而，由于空域法存在较多人为性的假设且随着近年来并行计算机技术的飞速发展及各种快速算法的广泛应用，计算量的大小不再是制约地球重力场反演精度的重要因素，时域法的优点正逐渐体现于地球重力场反演之中。时域法主要包括四种类型：（1）Kaula线性摄动法[6]，仅适合于求解低阶地球重力场且计算精度较低。（2）加速度法[7]，优点是基于数值微分原理有利于提高中高频地球重力场的感测精度；缺点是在差分掉双星共同误差的同时，也差分掉了部分地球重力场的低频信号，因此降低了重力场长波信号的灵敏度。（3）动力学法[8]，优点是求解精度较高；缺点是将卫星轨道参数对引力位系数偏微分的初值设定为零违背了天体运动的物理规律，求解过程复杂程度较高且需要高性能的并行计算机支持。（4）能量守恒法[9]，优点是观测方程物理含义明确且易于地球重力场的敏感度分析；缺点是对卫星轨道的测量精度要求较高。

表 1 卫星地球重力场模型[10]

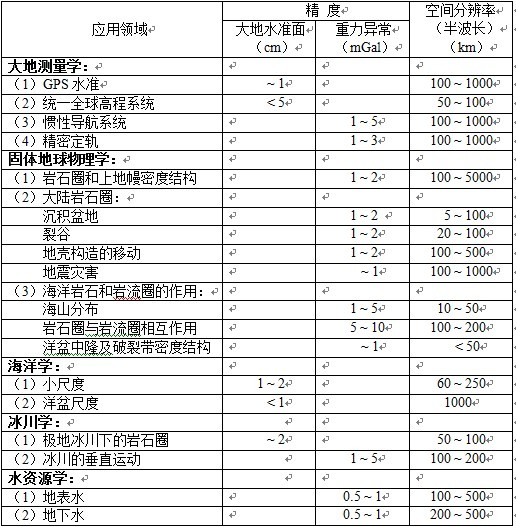
至今为止，国际众多科研机构基于车载、船载、机载和星载重力观测数据利用空域法和时域法已建立了不同精度和阶次的全球重力场模型（如表1所示），但由于各种地球重力场反演方法自身的不足和局限性，仅仅依靠各种方法的自我完善已无法满足本世纪相关学科对地球重力场精度进一步提高的迫切要求（如表2所示），因此寻求新的、高精度的、高空间解析度的、全频段的和快速的全球重力场反演方法是本世纪国际地球物理学和大地测量学界正面临的挑战和亟待解决的难题。此项科学难题的研究将为未来国际GRACE Follow-On和GOCE Follow-On地球重力卫星测量计划、GRAIL（Gravity Recovery and Interior Laboratory）月球重力双星探测计划和太阳系火星及其它行星探测计划中高精度和高阶次全球重力场模型的有效和快速确定提供理论基础和计算保证。目前国内外地球物理学和大地测量学界紧跟国际卫星重力测量的热点和动态，正积极投身于基于卫星重力测量建立下一代高精度和高阶次全球重力场模型的研究当中。

表2 相关学科对地球重力场反演精度需求[10]

 

参考文献

[1] http://www-app2.gfz-potsdam.de/pb1/op/grace/index_GRACE.html

[2] 许厚泽. 卫星重力研究: 21世纪大地测量研究的新热点 [J]. 测绘科学, 2001, 26(3): 1～3

[3] HAN S C, SHUM C K, BEVIS M, et al. Crustal dilatation observed by GRACE after the 2004 Sumatra-Andaman earthquake [J]. Science, 2006, 313(5787): 658～662

[4] MIGLIACCIO F, REGUZZONI M, SANSO F. Space-wise approach to satellite gravity field determination in the presence of colored noise [J]. Journal of Geodesy, 2004, 78(4): 304～313

[5] ZHENG W, XU H Z, ZHONG M, et al. Efficient and rapid estimation of the accuracy of GRACE global gravitational field using the semi-analytical method [J]. Chinese Journal of Geophysics, 2008, 51(6): 1143～1150

[6] CHENG M K. Gravitational perturbation theory for intersatellite tracking [J]. Journal of Geodesy, 2002, 76(3): 169～185

[7] DITMAR P, KUZNETSOV V, VAN ECK VAN DER SLUIJS A A, et al. DEOS CHAMP-01C 70: a model of the Earth’s gravity field computed from accelerations of the CHAMP satellite [J]. Journal of Geodesy, 2006, 79(10): 586～601

[8] REIGBER CH, SCHMIDT R, FLECHTNER F. An Earth gravity field model complete to degree and order 150 from GRACE: EIGEN-GRACE02S [J]. Journal of Geodynamics, 2004, 39(1): 1～10

[9] ZHENG W, SHAO C G, LUO J, et al. Numerical simulation of Earth’s gravitational field recovery from SST based on the energy conservation principle [J]. Chinese Journal of Geophysics, 2006, 49(3): 644～650

[10] 郑  伟. 基于卫星重力测量恢复地球重力场的理论和方法 [D]. 武汉: 华中科技大学, 2007, 1～136

 

(郑伟，许厚泽，钟敏供稿)