1 引 言
卫星重力测量技术的实现是继美国GPS星座成功构建之后在大地测量等交叉领域的又一项创新和突破,它之所以被国际大地测量学界公认为是当前地球重力场探测研究中最高效、最经济和最有发展潜力的方法之一,是因为它既不同于传统的车载、船载和机载重力测量,也不同于卫星测高和轨道摄动分析,而是通过卫星跟踪卫星(SST)和卫星重力梯度(SGG)恢复高精度和高空间分辨率的全球重力场[1]。SGG是国际大地测量学界创新提出的又一项探测地球重力场特性特征、精细结构和演变过程的新技术和新领域,目前它已逐渐发展成为专门研究空间重力梯度测量的理论、方法、载荷和应用的新兴科学。SGG在基础科学研究(如大地测量学、地球物理学、地震学、海洋学、惯性导航学、空间微重力学等)和国防建设领域都具有极其重要的科学意义和应用前景[2,3]。
探测和研究地球重力场精细结构是地球科学的基础性工作,也是大地测量学的主要科学任务之一。本世纪空间技术、惯性导航技术和卫星定位技术的快速发展以及地球深部结构和动力过程的深入研究,不仅对了解重力场精细结构提出了更高层次的需求,而且进一步明确了通过大地测量研究重力场的科学目标,使物理大地测量面临着新的挑战。本世纪目标是在全频段确定cm级精度大地水准面,而目前全球中高频大地水准面精度与此要求至少还相差一个量级。纵观现有重力测量技术的发展潜力:首先,SST模式仅适于确定中长波(2 ~ 120阶)地球重力场,由于其观测量是重力异常产生的轨道摄动,同时由于未采用无阻尼补偿技术(Drag-free)和卫星轨道高度无法进一步降低,因此中短波重力场恢复精度难以达到cm级;其次,由于卫星轨道覆盖在地球南北极存在测量空白区、若干高阶次引力位系数之间强相关产生的混叠和共振影响等缺点,只有精心设计多种不同卫星轨道倾角和运行周期的卫星群联合测量才能解决,而要发射大量轨道根数互补的重力卫星从经济角度考虑得不偿失[4]。SGG的优点是直接测定地球引力位的二次微分,其结果是将球谐系数放大了倍,因此可有效抑制地球引力位随高度的衰减效应,直接确定高阶次地球重力场的精细结构。近年来,为了进一步提高地球重力场的精度和空间分辨率,国际众多科研机构已相继于2000年7月15日和2002年3月17日成功实施了基于SST模式的CHAMP和GRACE重力卫星计划。但由于轨道高度和测量模式的局限性,其对中高频地球重力场信号的敏感性较弱。为了弥补CHAMP和GRACE的不足进而达到高精度恢复全频段地球重力场的目的,GOCE重力梯度卫星已于2009年3月17日成功发射,其对空间分辨率为100 km的大地水准面的测量精度优于1 cm[5]。
2 卫星重力梯度测量研究
2.1 重力梯度测量原理
自20世纪70年代末开始,国际大地测量学界的众多研究机构基于SGG测量原理、技术模式、误差分析、数据处理等方面开展了大量的数值模拟研究。经过30多年的潜心研究和需求论证,SGG原理已趋向成熟。自20世纪初以来,重力梯度测量原理从早期的扭力测量发展到目前的差分加速度测量。前者通过测定作用于检测质量的力矩来间接获取重力梯度值;后者通过测量两加速度计之间的加速度差来获得重力梯度观测值,可消除加速度计之间大部分公共误差的影响,因此较前者更有发展前景。目前SGG主要采用差分加速度测量原理。
2.2 重力梯度仪研究进程
重力梯度测量技术的创新和突破极大地推动了重力梯度仪的迅速发展。随着电子技术、计算机技术、低温超导技术等的发展,重力梯度仪在灵敏度和稳定性方面均有显著提升。重力梯度仪的研究大致经历了从单轴旋转到三轴定向,从室温到超低温(<4.2 K),从扭力、静电悬浮到超导的发展过程,仪器灵敏度日益提高[6,7]。20世纪初期,匈牙利物理学家建立了第一台重力梯度仪(扭秤),主要用于地球表面引力位二阶张量的测量(1E=10-9 s-2);20世纪中叶,扭秤逐步被易于操作的相对重力仪(如LaCoste,测量精度0.5 µGal,1 Gal=10-2 m/s2)替代;20世纪70年代末,美国宇航局(NASA)提出了SGG 的远期重力场飞行计划Gravity B,其最终目标是获得空间分辨率25 km,重力异常精度10-6 m/s2的全球重力场;20世纪80年代,法国提出了GRADIO计划,星载重力梯度仪灵敏度为10-2 E/Hz1/2;20世纪90年代,欧空局(ESA)制定了ARISTOTELES计划,星载重力梯度仪灵敏度为10-3 E/Hz1/2 ;20世纪90年代中期,ESA提出了GOCE卫星重力梯度计划,星载重力梯度仪测量精度为3×10-3 E;21世纪初期,NASA启动了超导重力梯度测量计划(SGGM),其科学目标是以50 km的空间分辨率和2 ~ 3 mGal的重力异常精度确定360阶地球重力场;近几年,美意两国正在研究系留卫星系统(TSS),星载重力梯度仪精度为10-6 E/Hz1/2,可望获得25 km的空间分辨率和1 ~ 2 mGal的重力异常精度。
2.3 卫星重力梯度仪的技术特征
卫星重力梯度仪是一种能直接探测空间重力加速度矢量梯度的传感器。由于重力梯度可以较好地反映等位面的曲率和力线的弯曲程度,因此敏感于中短波地球重力场的信号,更能反应重力场的精细结构。在地球卫星内的微重力环境中,由于不同位置点加速度的差异较小,因此不同属性的重力梯度仪通常由1 ~ 3对属性相同的加速度计按不同的排列方式组合而成,精确测定每对加速度计检验质量之间的相对位置变化,通过观测重力加速度的差进而得到重力梯度张量,此为SGG能在微重力环境下直接测量地球重力场参数的主要原因。目前重力梯度仪主要包括旋转式重力梯度仪(RGG)、静电悬浮重力梯度仪(ESG)、超导重力梯度仪(SGG)、量子重力梯度仪(QGG)等。旋转式重力梯度仪比较适合自旋稳定的小卫星,而新一代重力探测卫星通常为非自旋稳定的且旋转式重力梯度仪精度相对较低,因此较少用于SGG。将来国际SGG工程的发展方向以采用静电悬浮重力梯度仪、超导重力梯度仪、量子重力梯度仪等为主流。
(1)静电悬浮重力梯度仪
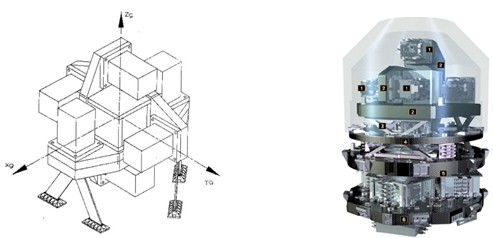
图1 静电悬浮重力梯度仪组件图[8]
GOCE卫星采用的静电悬浮差分重力梯度仪(如图1所示)由三对静电悬浮三轴加速度计对称排列组成,每个加速度计均设计为2个高灵敏轴和1个低灵敏轴,主要测定5个独立引力梯度分量中的4个(Vxx, Vyy, Vzz和Vxz)。重力梯度仪的质心与卫星体质心相距10 cm,长1320 mm,直径850 mm,重137 kg,基线长0.5 m,测量精度3×10-3 E/Hz1/2。测量原理是利用卫星内固定基线上的差分加速度计检验质量之间的重力加速度差值得到三维重力梯度张量。重力梯度仪的三轴指向与卫星体坐标系严格一致,不仅测量线性加速度,同时测量角加速度、离心力加速度、科里奥利(Coriolis)加速度以及其它扰动加速度。静电悬浮重力梯度仪具有结构简单、成本低、灵敏度高、抗外界干扰能力强、易于自动化数据采集等优点[9,10]。
(2)超导重力梯度仪
超导重力梯度仪由三对超导加速度计对称排列构成。如图2所示,单轴超导加速度计由弱弹簧、超导检测质量、电磁传感器和超导量子干涉仪(SQUID)组成。SQUID以10-16 m的精度测定超导检测质量的位移变化,电磁传感器所产生的磁场被超导检测质量的运动调制并由SQUID检测放大,最后转化为电压信号输出。类似于静电悬浮重力梯度仪,超导重力梯度仪可测定重力梯度张量的所有分量,同时用于改正运动平台的线性加速度和角加速度。在同轴分量系统中,信号正比于对角线元素和线性加速度(平移),而交叉分量系统则传递非对角线元素和角加速度(旋转),通过加速计不同方式的组合可确定对角线分量和全部分量。超导重力梯度仪与静电悬浮重力梯度仪相比,仅在加速度计测量原理上存在差别,前者用超导检测质量代替后者的电磁检测质量,用超导量子干涉仪代替电容装置来测量检测质量的位移,而重力梯度测量原理基本相同。由于超导感应检测质量的位移比静电悬浮法具有更高的灵敏度,因此超导重力梯度仪比静电悬浮重力梯度仪具有更大的发展潜力。
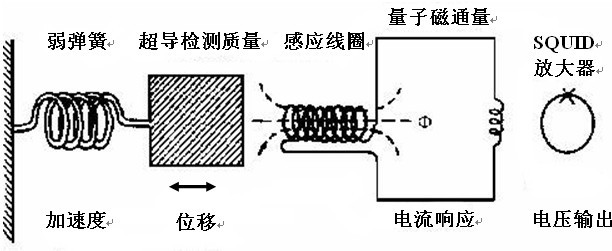
图2 单轴超导加速度计示意图
(3)量子重力梯度仪
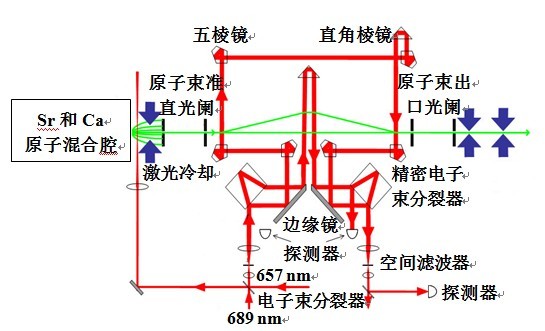
图3 原子干涉测量原理图
诺贝尔物理学奖得主、中国科学院外籍院士、美籍华人物理学家朱棣文教授领导的研究团队通过“坠落”原子精确测算出了单个原子的重力加速度,并得到重力加速度与宏观物体所受重力加速度相同的结论。此发现被物理学界称为“比萨斜塔实验”的现代版。量子重力梯度仪由1 ~ 3对原子干涉加速度计两两相互垂直排列组成(测量精度10-7 E/Hz1/2)。原子干涉加速度计是重力梯度仪的核心部件,与静电悬浮重力梯度仪和超导重力梯度仪存在本质上的区别。如图3所示,基本原理如下:首先利用激光将大量铯原子冷却至超低温度,在超低温状态下通常以超音速运动的原子速度将降低至1 cm/s左右,使测量其位置和速度变得更为容易;其次,将缓慢运动的原子置于重力场中做类似自由落体的“坠落”;最后,基于原子在激光作用下会形成相互重叠干涉的不同量子态的原理,利用原子受重力场作用前后所引起的相位差精确测出重力加速度。由于量子重力梯度仪对周围环境的质量分布极为敏感,因此它将有望为未来高精度和高空间分辨率地球重力场的探测带来革命性的影响。
2.4 卫星重力梯度测量的特点
(1)高精度和高空间分辨率解算中高频地球重力场。传统卫星重力技术一般只能恢复重力场的低频分量,而SGG张量可直接感测引力位的二阶梯度,进而获得较高阶次重力场精细结构的信息。模拟研究表明:当引入卫星轨道误差1 cm和卫星重力梯度值误差3×10-12 /s2,在250阶处恢复GOCE累计大地水准面的精度为9.025 cm。因此,卫星重力梯度测量是精化中短波重力场的有效途径之一。
(2)全球重力场测定速度快、代价低和效益高。实施卫星重力梯度测量的单颗卫星在近圆、近极和低轨道上连续飞行可获得全球覆盖和规则分布的重力梯度数据,其密度和分布取决于卫星飞行的时间、数据采样间隔、轨道参数等。GOCE重力梯度卫星在250 km低轨道上作20个月的绕地球飞行,基于1 s数据采样间隔可获得约5200万个重力梯度实测数据,全球观测数据空间分辨率可达到。从观测数据的精度、密度和分布来看传统卫星重力技术均难以达到,因此SGG是一种低代价、高效益和高效率测定全球重力场的技术。
(3)不受惯性加速度的影响。从重力梯度测量中有效分离出引力梯度张量不仅在理论上是严格的,而且在实际操作中也是可行的。因此,利用SGG技术可有效解决引力加速度与惯性加速度的分离问题。
(4)直接测定引力场的内部结构。据广义相对论可知,当有引力场存在时,四维时空是弯曲的黎曼空间。黎曼曲率张量刻画了该空间的几何结构,其主要分量与引力位的二阶导数成正比,因此测定引力位的二阶导数实际等价与测定四维时空的几何结构。从此意义上讲,SGG揭示了引力场的物理性质和几何性质之间的相互关系。
(5)大气阻力对重力梯度观测信号的影响较小。由于重力梯度观测信号是通过每对加速度计的输出量之差求得的,只要每对加速度计的性能指标尽可能一致,则大气阻力对每对加速度计的影响就基本相同,因此差分后的重力梯度观测信号可以基本上消除大气阻力的影响。
(6)仪器灵敏度和稳定度较高。静电悬浮技术和低温超导技术的成功应用,使重力梯度仪在灵敏度和稳定度方面有了较大的提高,特别是低温超导重力梯度仪具有零漂低、尺度因子稳定和灵敏度高的特性,测量精度可达10-4 E ~ 10-6 E。
(7)对卫星定轨精度要求较低。基于卫星轨道摄动分析的传统卫星重力测量技术主要取决于卫星定轨精度的高低,而SGG对定轨精度的要求相对较低。其原因是加速度计阵列本身可测定卫星的运动姿态,而且重力梯度数据的后处理可进一步改善卫星定轨的精度。
(8)SGG能感测重力梯度张量的所有分量。由于不同的卫星重力梯度张量反应不同的地球重力场信息,因此在地球物理解释中采用重力梯度张量比用重力标量将得到更丰富的地壳深部构造信息。
参考文献
[1] 许厚泽. 卫星重力研究: 21世纪大地测量研究的新热点 [J]. 测绘科学, 2001, 26(3): 1-3.
[2] 许厚泽, 周旭华, 彭碧波. 卫星重力测量 [J]. 地理空间信息, 2005, 3(1): 1-3.
[3] 郑伟, 许厚泽, 钟 敏, 员美娟, 周旭华, 彭碧波. 我国将来卫星重力梯度计划的实施. 中国地球物理2009年刊, 合肥: 中国科学技术大学出版社, 2009, 709-710.
[4] 郑伟. 基于卫星重力测量恢复地球重力场的理论和方法 [D]. 武汉: 华中科技大学, 2007, 1-139.
[5] 郑伟, 许厚泽, 钟 敏, 员美娟, 周旭华, 彭碧波. 国际卫星重力梯度测量计划研究进展. 测绘科学, 2010, 35(2): 57-61.
[6] van Gelderen M, Koop R. The use of degree variances in satellite gradiometry [J]. Journal of Geodesy, 1997, 71(4): 337-343.
[7] Albertella A, Migliaccio F, Sanso F. GOCE: the Earth gravity field by space gradiometry [J]. Celestial Mechanics and Dynamical Astronomy, 2002, 83(1): 1-15.
[8] http://www.esa.int/esaLP/LPgoce.html.
[9] Sneeuw N, van den IJssel J, Koop R. Validation of fast pre-mission error analysis of the GOCE gradiometry mission by a full gravity field recovery simulation [J]. Journal of Geodynamics, 2002, 33(1): 43-52.
[10] Muller J, Wermut M. GOCE gradients in various reference frames and their accuracies [J]. Advances in Geosciences, 2003, 1: 33-38.




